Home > Research > Augmented Uniform Polyhedra
Prev (Enumeration) Next (Cut Equilateral Triangle In 6)

Augmented Uniform Polyhedra

I wanted to find more polyhedra that looked like the uniform polyhedra. Norman Johnson had already enumerated all the convex regular-faced polyhedra, so I thought I'd consider the nonconvex ones. There are an infinite number of these, so some further rules are required to find the interesting ones. I considered these two additional rules:

  1. Must be locally-convex. That is, the faces surrounding each vertex must loop around the vertex in the same direction (no retrograde faces spanning back the other way).
  2. All vertices must be vertices of the convex hull. This is to ensure that all vertices are visible, and is a condition always met by uniform polyhedra.
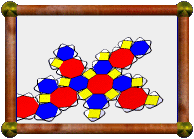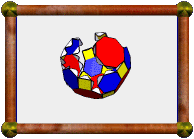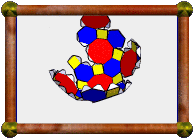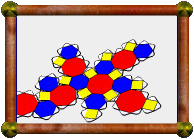
Various existing polyhedra already follow these rules, eg some nonconvex cupolae, pyramids, etc. But remembering that none of the Johnson Solids have higher than dihedral symmetry, I wondered if any of this new class of polyhedra might. So better-than-dihedral symmetry became a third rule. After a while I thought of what should have been an obvious course for investigation. The uniform polyhedra already satisfy the rules, so why not try augmenting some of their faces with pyramids or cupolae? This turned out to be fruitful, although initially it only lead to four new polyhedra in this class: one with octahedral symmetry, and three with icosahedral symmetry. They are pictured below:

Augmented Great Cubicuboctahedron Augmented Dodecadodecahedron Augmented Great Ditrigonal
Dodecicosidodecahedron		 Augmented Snub
Dodecadodecahedron

In the three icosahedral cases, the pentagons are augmented with pentagonal pyramids, in the other case the squares are augmented with square pyramids. Unfortunately, augmenting with cupolae failed to meet the conditions in all cases.

More interesting new polyhedra could surely be created by changing my rules slightly.

Since my initial investigation, Jim McNeill has taken this idea and run with it. He found many more polyhedra following these rules and variations on them. His results can be found at http://www.orchidpalms.com/polyhedra/uniform/augmented/augment.html.

Home > Research > Augmented Uniform Polyhedra
Prev (Enumeration) Next (Cut Equilateral Triangle In 6)