

| Home > Gallery > My Models > 4D Cross-Sections > 0.18 Cross-Section of Great Icosahedral 120-Cell | |
| Prev (0.5 Cross-Section of Great Stellated 120-Cell) | Next (Pentagonal Cupola (J5)) |
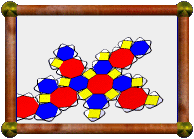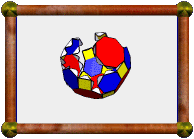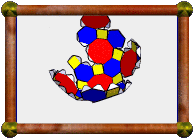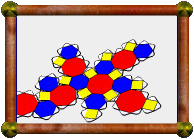
0.18 Cross-Section of Great Icosahedral 120-Cell |

| Like or comment on facebook |
The great icosahedral 120-cell is number 14 in the list of uniform polychora in Stella4D, with the abbreviated name "gofix". It is a regular polychoron, with 120 great icosahedra as its cells. 12 such cells meet at each vertex, forming a small stellated dodecahedral vertex figure. The model you see here is a 3D cross-section through that 4D polytope, taken 18% of the way through the model, along one of the 60 icosahedral symmetry axes.
The model consists of 13 small stellated dodecahedra: a regular one at the centre (representing the first vertex sliced by the sectioning plane), and 12 distorted ones around the outside, each with one spike that intersects one of the spikes of the central polyhedron. The distorted ones represent cross-sections through vertices at an angle, causing the distortion.
It makes a striking model, looking like some sort of alien weapon or space craft!
See this tutorial for some comments on obtaining nets for building paper models of 4D polytopes.

|
The faces of this 3D cross-section are themselves 2D cross-sections of the great icosahedron. First, there are small, medium and large regular pentagrams, representing cross-sections orthogonal to the 5-fold symmetry axes of the great icosahedron (largest pentagram outlined here). |

|
Secondly, there are small distorted pentagrams, near the outside of the model, occurring two-per-plane. These represent cross-sections orthogonal to the 2-fold axes. Such sectioning planes will slice two vertices of the great icosahedron at once, generating two faces per plane. |

|
Finally, there are some larger distorted pentagrams poking into the central small stellated dodecahedron. These occur 3-per-plane and represent cross-sections orthogonal to the 3-fold symmetry axes. Such planes will cut through 3 vertices at once. |

|
I started down the wrong path when making this model. I originally planned to attach the spikes together as shown, with each spike truncated to leave a pentagon, and the two parts glued together at this flat face. I decided this would be a bad idea, not giving enough strength at the narrow join. So I started again! I also didn't like my colour choice so took the opportunity to give the whole thing a more menacing metallic look! |

|
Instead of a flat join, I allowed full length spikes on the outer parts, and built inverted spikes for them to sit in on the inner part. |

|
When the outer parts have their spikes glued into these cups, it should form a strong join. Handy if I want to pick this thing up by just one of the outer parts! |

|
I added a pentagon across the base of each section for strength, but had to leave a hole for the outer spikes to stick through. |

|
Put these sections together like a dodecahedron to complete the central part. |

|
Here are the different types of nets for the outer parts (distorted small stellated dodecahedra). |

|
Again, I strengthened them with pentagonal parts at the base of each spike. |

|
Make 12 such parts and you're ready to glue them into the central part. |

|
Ready for battle! |

|
Each part fits snuggly into the central cups. Just put glue around the inside of the cups and hold the outer parts in. |

|
Another photo of the finished model. |

|
Close-up. |

|
Another close-up. |

|
Here's the model on display at the Bridges 2016 conference in Jyväskylä, Finland. |


| Like or comment on facebook |
| Home > Gallery > My Models > 4D Cross-Sections > 0.18 Cross-Section of Great Icosahedral 120-Cell | |
| Prev (0.5 Cross-Section of Great Stellated 120-Cell) | Next (Pentagonal Cupola (J5)) |