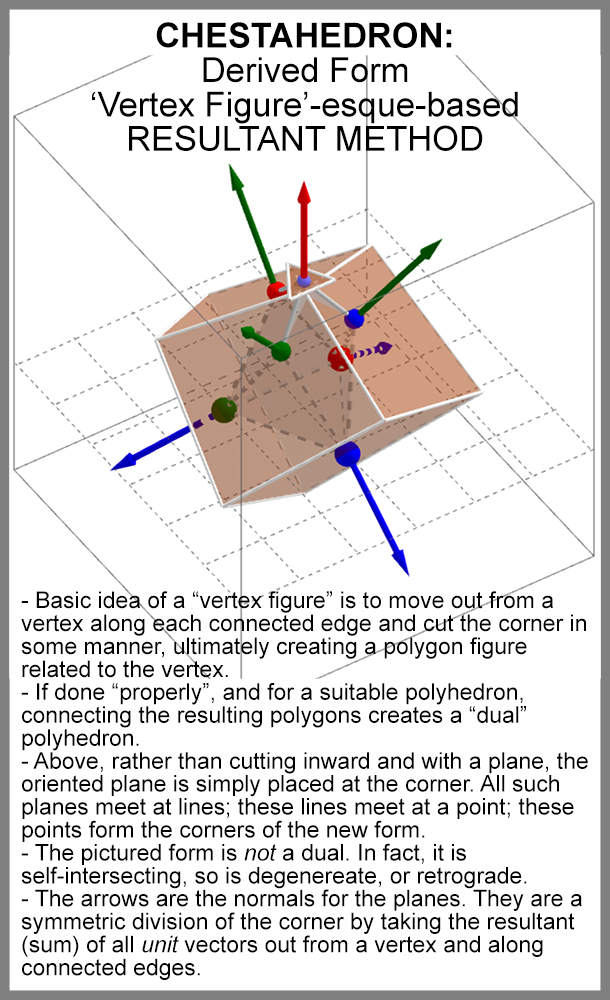
The canonical triangular antihermaphrodite isn't the only form with a midsphere (consider the form with four equilateral triangles and the dihedral angle of an icosahedron at the base) . If you scale the chesterhedron model to make the edge-tangent ellipsoid into a sphere it won't necessarily transform the chesterhedron into the canonical form. To check the case here, the antihermaphodite has vertices at two heights above the base, and I make it that the ratio of these two heights in the canonical form is different to the chesterhedron, and so I don't believe they can be transformed into each other by scaling.guy wrote:Going back to the canonical construction of the solid and its dual, we can readily see that your Chestahedron/ellipsoid construction is a simple stretching of the canonical construction and that symmetries relating to the stretching axis are preserved. In particular, the relative volumes and proportions of the polyhedron and its dual are preserved: they remain congruent. That is, the dual of your Chestahedron, obtained by reciprocation in an edge-tangent ellipsoid, is congruent to the Chestahedron - in short, it is self-dual about the ellipsoid.
Also, consider that reciprocating in the ellipsoid will produce perpendicular dual edges at the same tangency points. For the chesterhedron to be self-dual in the ellipsoid, the upper and lower ring of tangency points would need to have the same radius, and this is not the case from the image posted.