How hard would it be to compute true filling?
-
metachirality
- Posts: 12
- Joined: Fri Dec 20, 2019 10:02 pm
How hard would it be to compute true filling?
True filling is filling regions of a polytope if they can be continuously transformed into a region of odd density. How feasible is this in practice?
- robertw
- Site Admin
- Posts: 732
- Joined: Thu Jan 10, 2008 6:47 am
- Location: Melbourne, Australia
- Contact:
Re: How hard would it be to compute true filling?
Wouldn't that mean they are already odd density? Can an even-density region ever be transformed to an odd density?
Did you already find "Display->Polygon Filling Options" from the menu? What you want is similar to the Modulo-2 method.
Did you already find "Display->Polygon Filling Options" from the menu? What you want is similar to the Modulo-2 method.
-
metachirality
- Posts: 12
- Joined: Fri Dec 20, 2019 10:02 pm
Re: How hard would it be to compute true filling?
No, I mean if you had a four-shaped thing and transformed it so that it didn't intersect itself, you would've transformed the even density region in the four's intersection into an odd density region.
- robertw
- Site Admin
- Posts: 732
- Joined: Thu Jan 10, 2008 6:47 am
- Location: Melbourne, Australia
- Contact:
Re: How hard would it be to compute true filling?
Do you mean something like this, with arms that cross over each other?
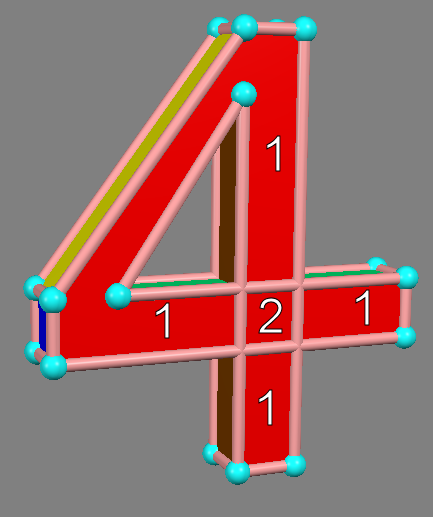
And then pull the arms apart so there's no more overlap?
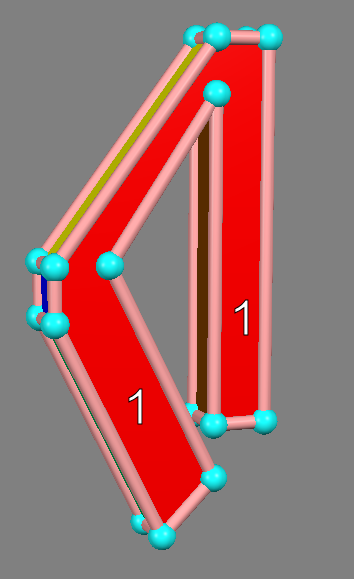
I guess the region of space that was once density 2 is now density 1, but you could simply move the whole object to transform any region of space between odd and even density. So maybe I'm still not sure what you mean.
My way of thinking about density would be as follows. As the shape is transformed, the region 2 density shrinks until it disappears. It can never transform to an odd-density region without faces crossing over it.
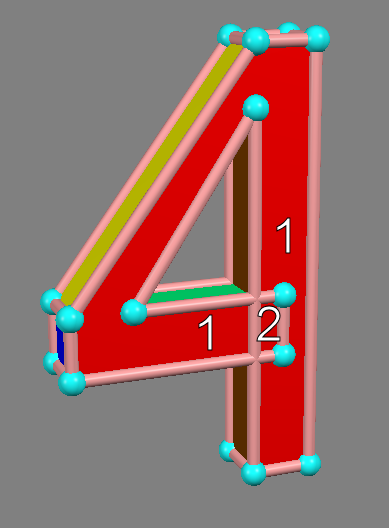

And then pull the arms apart so there's no more overlap?

I guess the region of space that was once density 2 is now density 1, but you could simply move the whole object to transform any region of space between odd and even density. So maybe I'm still not sure what you mean.
My way of thinking about density would be as follows. As the shape is transformed, the region 2 density shrinks until it disappears. It can never transform to an odd-density region without faces crossing over it.

-
metachirality
- Posts: 12
- Joined: Fri Dec 20, 2019 10:02 pm
Re: How hard would it be to compute true filling?
The empty space around the polyhedron is also considered as a region. For orientable polyhedra, this is the same as density filling, for non-orientables its more complicated. For uniform polyhedra I think that binary filling works, but for other polyhedra which are non-orientable but not uniform, it's different.
- robertw
- Site Admin
- Posts: 732
- Joined: Thu Jan 10, 2008 6:47 am
- Location: Melbourne, Australia
- Contact:
Re: How hard would it be to compute true filling?
My understanding is that for orientable polytopes, the density of a region will stay the same however the shape is transformed provided no facets pass over the region. For non-orientables, there is only odd and even density (1 or 0), but still regions will remain odd or even unless a facet passes over them. I suspect also that any even density region in a non-orientable can be transformed to the exterior of the model, but I don't think that's been proven.
Re: How hard would it be to compute true filling?
The issue here is, how do you define a "region"? When you pull apart the vertical and horizontal ends of the 4, are you pulling the horizontal away from the vertical, or are you pulling the vertical away from the horizontal? In each case, where does the region of density=2 go?
Conventionally, we say that the region shrinks to zero and disappears. If you wish to nail certain parts of your polyhedron to the background and just morph other bits of it, then you need to explicitly define this. And you will still need to distinguish between regions relative to the containing space vs. regions relative to the polyhedral surface.
Hope this helps clarify the underlying confusions behind the question.
Cheers,
Guy. Guy's polyhedra pages
Guy. Guy's polyhedra pages
- robertw
- Site Admin
- Posts: 732
- Joined: Thu Jan 10, 2008 6:47 am
- Location: Melbourne, Australia
- Contact:
Re: How hard would it be to compute true filling?
Sorry Guy, I didn't follow that. I don't see what the background has to do with it, or why it matters which part is dragged away from the other. Yes I would see the density-2 region as shrinking to zero and disappearing as the overlapping parts are moved apart.
Re: How hard would it be to compute true filling?
metachirality asked about regions suddenly flipping to a different density. I was trying to explain that using the conventional definition of a dense interior region, this cannot happen; as the polyhedron morphs, one region progressively gives way to another one of different density. A sudden flip can only happen if you define such a region in an unconventional way. The OP did not appear to be clear on this.
One may define a static region of space, such that when the polyhedron morphs it passes through the region. This is what I meant by nailing a region to the background. But it would be an unusual and complicated way to approach polyhedral density (which is possibly why my remarks are a little unusual and complicated).
One may define a static region of space, such that when the polyhedron morphs it passes through the region. This is what I meant by nailing a region to the background. But it would be an unusual and complicated way to approach polyhedral density (which is possibly why my remarks are a little unusual and complicated).
Cheers,
Guy. Guy's polyhedra pages
Guy. Guy's polyhedra pages
