Noble polyhedra. Where can I find them?
-
senkoquartz
- Posts: 50
- Joined: Wed May 20, 2020 1:41 pm
Noble polyhedra. Where can I find them?
I found out about noble polyhedra a few days ago. I was looking at the final icosahedron stellation and realized it's an isohedral isogonal figure made out of ENNEAGRAMS. THAT'S INSANE. Now my mission in life is to learn about all the noble polyhedra I can.
What I'm interested in are the "miscellaneous" ones that are neither disphenoids nor crown polyhedra - the ones with octahedral/icosahedral symmetry.
The problem is, finding them on the internet is extremely hard. They are alluded to, but never listed.
From what I gather, most of the known ones are found in Max Brückner's "Uber die gleichecking-gleichflachigen, diskontinuierlichen und nichtkonvexen Polyheder" (1906). But I can't find a .pdf online, or a place to buy it.
Where can I find them?
What I'm interested in are the "miscellaneous" ones that are neither disphenoids nor crown polyhedra - the ones with octahedral/icosahedral symmetry.
The problem is, finding them on the internet is extremely hard. They are alluded to, but never listed.
From what I gather, most of the known ones are found in Max Brückner's "Uber die gleichecking-gleichflachigen, diskontinuierlichen und nichtkonvexen Polyheder" (1906). But I can't find a .pdf online, or a place to buy it.
Where can I find them?
- robertw
- Site Admin
- Posts: 722
- Joined: Thu Jan 10, 2008 6:47 am
- Location: Melbourne, Australia
- Contact:
Re: Noble polyhedra. Where can I find them?
If you have Great Stella or Stella4D, then they can be found in the library, in the Bruckner folder:
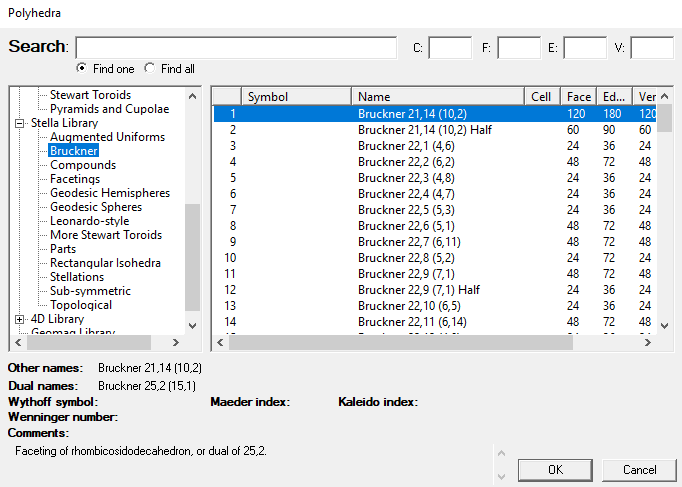
And since Stella shows you the dual as well, and nobles are all duals of other nobles, you get two at once:
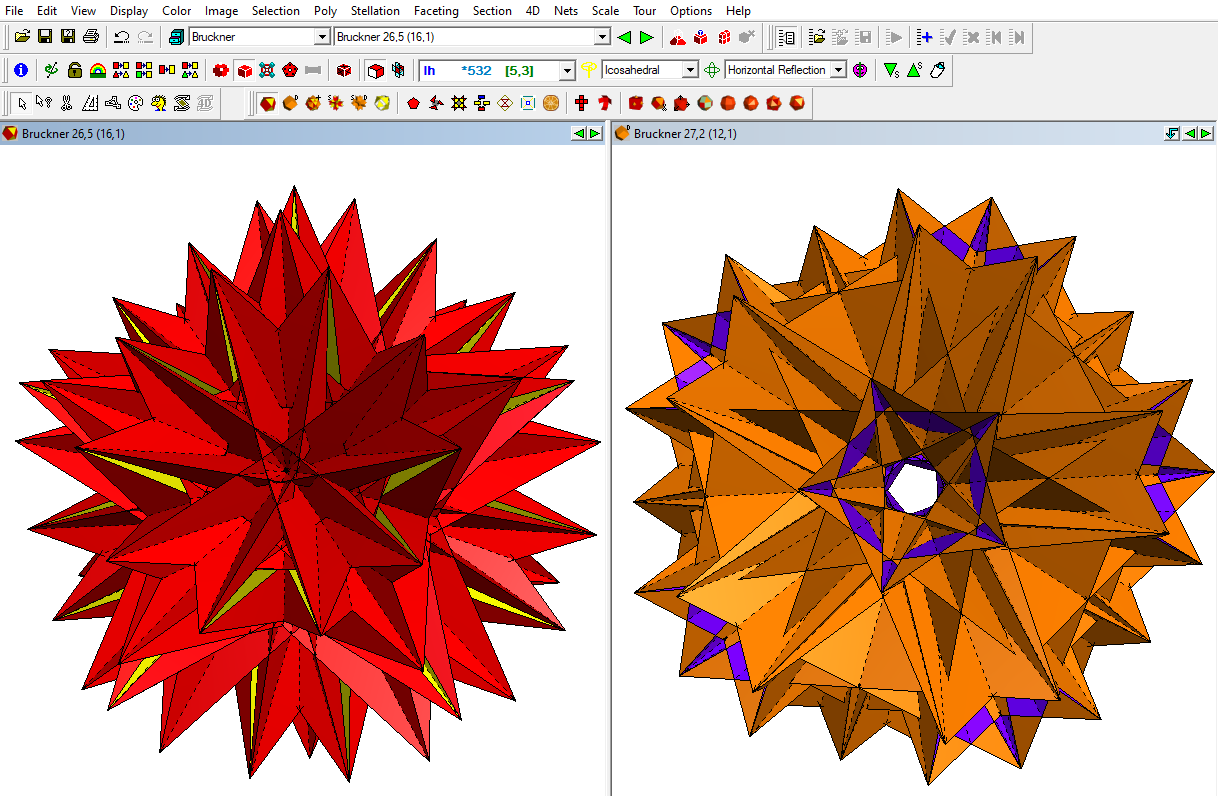
You'll even find my own more recent discovery in there. You can see a paper model here:
https://www.software3d.com/NobleSnub.php

And since Stella shows you the dual as well, and nobles are all duals of other nobles, you get two at once:

You'll even find my own more recent discovery in there. You can see a paper model here:
https://www.software3d.com/NobleSnub.php
-
senkoquartz
- Posts: 50
- Joined: Wed May 20, 2020 1:41 pm
Re: Noble polyhedra. Where can I find them?
@robertw
I bought it, and I'm enjoying it a lot. In the Bruckner catalogue, after sifting through compounds and dual entries, I count 27 distinct nobles with octahedral or icosahedral symmetry, not including another 8 with degenerate hexagonal faces.
In another thread you mentioned that you found a few novel noble polyhedra among Archimedean dual stellations, the "Noble Snub Cube Faceting" being one of them. What were the others? Were they degenerate or no?
I bought it, and I'm enjoying it a lot. In the Bruckner catalogue, after sifting through compounds and dual entries, I count 27 distinct nobles with octahedral or icosahedral symmetry, not including another 8 with degenerate hexagonal faces.
In another thread you mentioned that you found a few novel noble polyhedra among Archimedean dual stellations, the "Noble Snub Cube Faceting" being one of them. What were the others? Were they degenerate or no?
- robertw
- Site Admin
- Posts: 722
- Joined: Thu Jan 10, 2008 6:47 am
- Location: Melbourne, Australia
- Contact:
Re: Noble polyhedra. Where can I find them?
Although I added features to Stella to make them easy to find, I unfortunately never got around to publishing my results. But polyart on this forum is getting a paper published about them soon. I'll direct him to this thread, in case he hasn't seen it already.
They can be found as facetings of isogonal polyhedra, ie polyhedra whose vertices are all the same, such as the Archimedean solids or any of the uniform polyhedra (and some others). From the menu, select "Faceting->Faceting Criteria->Isohedral", then go to the Preview Faceting view and hit the up arrow to step through valid facetings. This will include compounds, but won't include polyhedra with faces that visit the same vertex more than once (which may or may not be acceptable to you. Bruckner allowed these). You've just got to sort out which ones are compounds, generally by converting the faceting preview into the base model and seeing if it colours it as a compound.
They can be found as facetings of isogonal polyhedra, ie polyhedra whose vertices are all the same, such as the Archimedean solids or any of the uniform polyhedra (and some others). From the menu, select "Faceting->Faceting Criteria->Isohedral", then go to the Preview Faceting view and hit the up arrow to step through valid facetings. This will include compounds, but won't include polyhedra with faces that visit the same vertex more than once (which may or may not be acceptable to you. Bruckner allowed these). You've just got to sort out which ones are compounds, generally by converting the faceting preview into the base model and seeing if it colours it as a compound.
Re: Noble polyhedra. Where can I find them?
In my paper paper for this year‘s Bridges Conference in Helsinki (which has been cancelled due to corona) I describe how I used Stella4D to create noble polyhedra. I did it in the way Robert mentioned above and which is very easy to do. I was only interested in distinct ones, not in componds. I found 61 shapes, 19 of them were previously unpublished. Some of Brückner‘s models could not be reproduced and from the truncated icosidodecahedron no isohedral faceting was available. So there might be some more noble polyhedra to discover.
I‘ll post a link when the Bridges Proceedings 2020 are published
Ulrich
I‘ll post a link when the Bridges Proceedings 2020 are published
Ulrich
-
senkoquartz
- Posts: 50
- Joined: Wed May 20, 2020 1:41 pm
Re: Noble polyhedra. Where can I find them?
@Ulrich
I followed the above method - found 46 total.
There is a weird shape - not a noble - from faceting the 2 snub cubes compound. Face is a 7gon, with 2 types of vertices.
I followed the above method - found 46 total.
There is a weird shape - not a noble - from faceting the 2 snub cubes compound. Face is a 7gon, with 2 types of vertices.
Re: Noble polyhedra. Where can I find them?
I was able to reproduce this, it‘s really nice. Unfortunately it is only isohedral.
I sent you a table with my noble findings the other day in a private message, so that you can compare your list with mine.
Ulrich
I sent you a table with my noble findings the other day in a private message, so that you can compare your list with mine.
Ulrich
-
senkoquartz
- Posts: 50
- Joined: Wed May 20, 2020 1:41 pm
Re: Noble polyhedra. Where can I find them?
@Ulrich
When I said I found 46, I wasn't counting regular polyhedra and ones with degenerate faces - of which there are 17. So I actually have 3 new ones for you.
The first two are a dual pair with hexagram faces - the first one has the same convex hull as your W115_01_d in the .pdf sent me, and the second has the same convex hull as W115_02_d.

The third is a self-dual, same hull as W110_01_d.
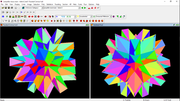
When I said I found 46, I wasn't counting regular polyhedra and ones with degenerate faces - of which there are 17. So I actually have 3 new ones for you.
The first two are a dual pair with hexagram faces - the first one has the same convex hull as your W115_01_d in the .pdf sent me, and the second has the same convex hull as W115_02_d.

The third is a self-dual, same hull as W110_01_d.

Re: Noble polyhedra. Where can I find them?
Very nice! I could construct them from W115_01_d resp. W110_01_d.
The faces of your third one are very similar to those of W96_01_sd, but
the stellation diagram is different.
Ulrich
The faces of your third one are very similar to those of W96_01_sd, but
the stellation diagram is different.
Ulrich
-
senkoquartz
- Posts: 50
- Joined: Wed May 20, 2020 1:41 pm
Re: Noble polyhedra. Where can I find them?
@Ulrich
Oh, I forgot - there was also this dodecahedron facet dual pair with degen vertices
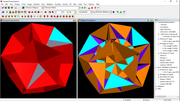
I'm interested in finding nobles with 120 vertices. When I try to facet a polyhedron with 120 vertices, Stella puts up a heroic effort but crashes before finishing searching for them. In any case, I don't know how to find them like Bruckner did.
The vast majority of the ~7000 semi-uniforms Jonathan Bowers found have 120 vertices. I wonder if the same is the case for noble polyhedra
Oh, I forgot - there was also this dodecahedron facet dual pair with degen vertices

I'm interested in finding nobles with 120 vertices. When I try to facet a polyhedron with 120 vertices, Stella puts up a heroic effort but crashes before finishing searching for them. In any case, I don't know how to find them like Bruckner did.
The vast majority of the ~7000 semi-uniforms Jonathan Bowers found have 120 vertices. I wonder if the same is the case for noble polyhedra
Re: Noble polyhedra. Where can I find them?
It is that truncated icosidodecahedron problem that I mentioned above. Stella can‘t handle it because there are too many data.
Some of the Brückner polyhedra with 120 vertices from the library can be used as source for new noble ones and stella doesn‘t crash. But all of them have only 60 vertices and most of them are compounds.
Robert created the Brückner polyhedra by hand with an older program version where the automatic search for facetings wasn‘t possible. He did it according to the pictures and diagrams Brückner gave in his 1906 book. They can be found at Vladimir Bulatov‘s website:
http://www.bulatov.org/polyhedra/bruckn ... index.html
Some of the Brückner polyhedra with 120 vertices from the library can be used as source for new noble ones and stella doesn‘t crash. But all of them have only 60 vertices and most of them are compounds.
Robert created the Brückner polyhedra by hand with an older program version where the automatic search for facetings wasn‘t possible. He did it according to the pictures and diagrams Brückner gave in his 1906 book. They can be found at Vladimir Bulatov‘s website:
http://www.bulatov.org/polyhedra/bruckn ... index.html
-
senkoquartz
- Posts: 50
- Joined: Wed May 20, 2020 1:41 pm
Re: Noble polyhedra. Where can I find them?
For the past day I've been interested in rigidly symmetrical polyhedra in general.
(I'll be ignoring infinite dihedral families here.)
There are countless types of isogonal polyhedra (and their isohedral duals), but the ones that are rigid and lose their transitivity when distorted seem more unique and interesting, symmetrical.
Of the 18 isogonal vertex arrangements (ignoring prisms), only the dodecahedron and icosidodecahedron are rigidly isogonal - the others can slide around in a continuum. (The tetrahedron, cube and octahedron have prismatic symmetry, so they can get squashed and still have vert/face transivity.)
What's interesting is that the dodecahedron is isogonally rigid but isohedrally flexible, while the icosahedron is the inverse - vert-flexible and face-rigid.
And faceting and stellation are dual operations,
so if you facet the dodecahedron, you can get 20 isogonal-rigid results, and their duals yield 17 distinct isohedral-rigid stellations of the icosahedron.
The 17 icosahedron stellations look way more interesting and pretty than the docahedron facets IMO. I made a folder of them.
You can do the same process with the icosidodecahedron / rhombic triacontahedron pair, but the problem is there are 8000+ results, with heaps of similar cases, and crazy 13 or 14 or 24 sided faces, vertices lying wantonly lying on edges... I made a small sample folder.
Question: is there a way I can get stellations to *behave* and have proper polygon faces instead of these weird jaggy hollow things?
(I'll be ignoring infinite dihedral families here.)
There are countless types of isogonal polyhedra (and their isohedral duals), but the ones that are rigid and lose their transitivity when distorted seem more unique and interesting, symmetrical.
Of the 18 isogonal vertex arrangements (ignoring prisms), only the dodecahedron and icosidodecahedron are rigidly isogonal - the others can slide around in a continuum. (The tetrahedron, cube and octahedron have prismatic symmetry, so they can get squashed and still have vert/face transivity.)
What's interesting is that the dodecahedron is isogonally rigid but isohedrally flexible, while the icosahedron is the inverse - vert-flexible and face-rigid.
And faceting and stellation are dual operations,
so if you facet the dodecahedron, you can get 20 isogonal-rigid results, and their duals yield 17 distinct isohedral-rigid stellations of the icosahedron.
The 17 icosahedron stellations look way more interesting and pretty than the docahedron facets IMO. I made a folder of them.
You can do the same process with the icosidodecahedron / rhombic triacontahedron pair, but the problem is there are 8000+ results, with heaps of similar cases, and crazy 13 or 14 or 24 sided faces, vertices lying wantonly lying on edges... I made a small sample folder.
Question: is there a way I can get stellations to *behave* and have proper polygon faces instead of these weird jaggy hollow things?
-
senkoquartz
- Posts: 50
- Joined: Wed May 20, 2020 1:41 pm
Re: Noble polyhedra. Where can I find them?
*regarding that last question - i mean when I go through the 227 rhombic triacontahedron stellations for example, they outwardly look like isohedra but the faces are broken up
- robertw
- Site Admin
- Posts: 722
- Joined: Thu Jan 10, 2008 6:47 am
- Location: Melbourne, Australia
- Contact:
Re: Noble polyhedra. Where can I find them?
Stellations in Stella are found via combinations of stellation cells, and consist of only externally accessible faces (no hidden parts of faces). So it's not aware about how or whether facelets in the same plane can be combined into larger faces. So it's not good for finding isohedra. There are some stellation criteria to choose from, see https://www.software3d.com/PolyNav/Poly ... p#stelCrit. The "fully supported" criteria will avoid the hollow parts you mentioned, but may miss some things of interest too.
Better to do such searches using the Faceting view instead. This always forms proper faces between the existing vertices.
Better to do such searches using the Faceting view instead. This always forms proper faces between the existing vertices.
Re: Noble polyhedra. Where can I find them?
My paper about exploring noble polyhedra with Stella4D is now online at the Bridges Website:
http://archive.bridgesmathart.org/2020/ ... 20-257.pdf
Ulrich
http://archive.bridgesmathart.org/2020/ ... 20-257.pdf
Ulrich
