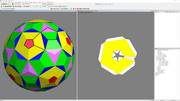
Yep getting all the pentagons planar will be an issue. Might be easier to aim for creating the dual instead, which will be mostly triangles with a few quads. Easier to keep them planar then.
I tried some things and ended up having some success. Here's what I did...
(1) Load a rhombicosidodecahedron (Ctrl+N for "new" and find it in the list, or type "rid")
(2) Stellate over the triangles and make it the new base model
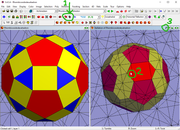
(3) The pentagons are too big here. I want to stellate over them but not all the way, so I added the model to a slightly larger dodecahedron, giving extra planes for the stellation. First I set the scale to 5 (Scale->Base Polyhedron Radius) and put it in a memory slot (Edit->Put Model in Memory->Memory 1, or type "m1"). Load a dodecahedron and set its scale to 6.5 (I tried a few different values). Add it to the previous model (Edit->Add/Blend from Memory). Then select stellation cells again to carve out the desired shape. Make this the new base model.

(4) Looking good, b ut we need to subdivide the hexagons into 4 pentagons. I found subdividing faces to level 6 was a good starting point. Then use faceting mode to create the faces. Accept the faceting, saying "No" to blending faces.
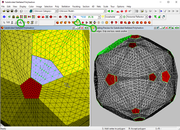
The faceting looks pretty good, but some of the pentagons are coplanar.
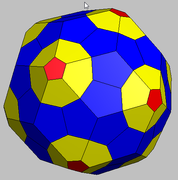
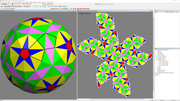
(5) I tried using the spring model to make faces closer to regular. It gave an interesting result but not what we want:

(6) Instead, I decided to make the dual we want. Select each face type in turn (3 of them) and augment with a pyramid, stretching each pyramid out a bit. We want all the peaks to lie roughly on a sphere (doesn't need to be exact). I got this:

(7) Create the convex hull and look at the dual

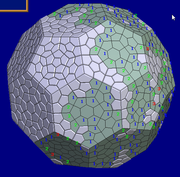
(8) It's what we want, but could be better. Make sure the base view is selected (just click in it) and use "Poly->Project Onto Sphere". This improves the dual a bit
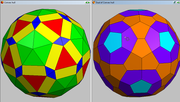
Not bad. There's a few choices a long the way that could improve it. Maybe try 6.6 or 6.7 in step 3 (7.0 was too much). And maybe better not to stretch the pyramids as far as I did in step 6.
No doubt Robert Austin's method was simpler!