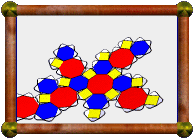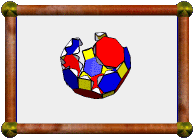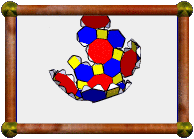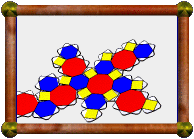
Compound of Cuboctahedron and Dual

Like or comment on facebook

This is a compound of the cuboctahedron and its dual, the rhombic dodecahedron. Notice how each vertex of one sits above a face of the other, and that edges from each cross at right-angles in pairs. The points where they cross lie on the shared midsphere of the two polyhedra, i.e. the edges are tangent to the midsphere at those points.

The model may be constructed in Great Stella by adding the cuboctahedron to its dual via the menu item "Poly>Add Base Model and Dual", or equivalently by going to the compound of base & dual view, and clicking the left-and-down button at the top of that view to use this compound as the new base model. Nets may then be displayed and printed.

	It's a compound of these two polyhedra.
	Just sticking pyramid tips onto the faces of either the cuboctahedron or its dual won't lead to the cleanest result. But here's a clever way to build a paper model, based on advice from Fr. Magnus Wenninger's book Polyhedron Models. Pieces may be made as shown, with long tabs to hold parts together that only touch at a point in the final model. These tabs span across potential weak points in the model where edges of the two polyhedra cross, keeping them in alignment and strengthening the model. To print these hollow faces, start with the cuboctahedron and use "Poly→Subdivide Faces" with a value of 2 so that points are printed half way along each edge. I also printed smaller squares and triangles to fit inside and add further strength.
	Attach the sections together like faces of a cuboctahedron.
	Another photo of the finished model.

Home > Gallery > My Models > Dual Compounds > Compound of Cuboctahedron and Dual
Prev (Compound of Truncated Tetrahedron and Dual)	Next (Compound of Icosidodecahedron and Dual)