Home > Research > Cut equilateral triangle into 6 congruent parts - no, not like that!
Prev (Augmented Uniform Polyhedra)	Next (Vertex Descriptions)

Cut equilateral triangle into 6 congruent parts - no, not like that!

It's fairly trivial to cut a regular N-gon into 2N congruent parts, as shown below. Congruent meaning that the pieces must all be the same shape and the same size, but reflection is allowed.

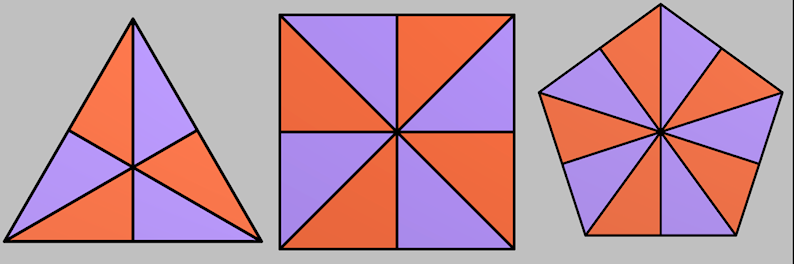
However, what if I asked you to find another way?

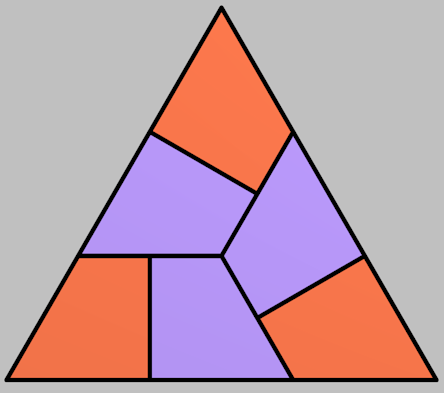
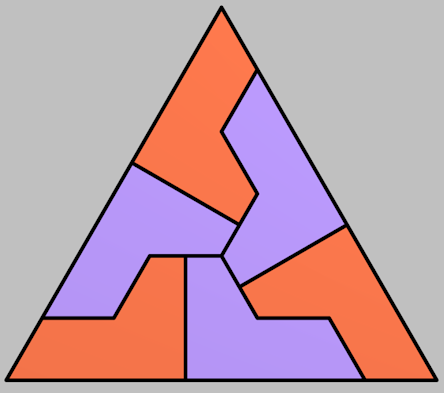
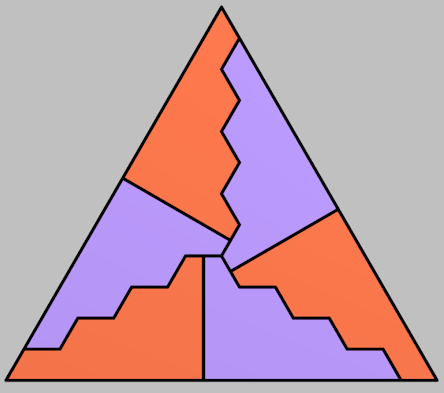
Let's start with the equilateral triangle. The next solution is trickier, but not too hard to come up with after some thought:

Click to reveal the second solution

But are there more ways? It gets much harder to find a solution after this, but I have found that there's actually an infinite series of solutions, and can in fact be done with pieces that are N-gons for any even N.

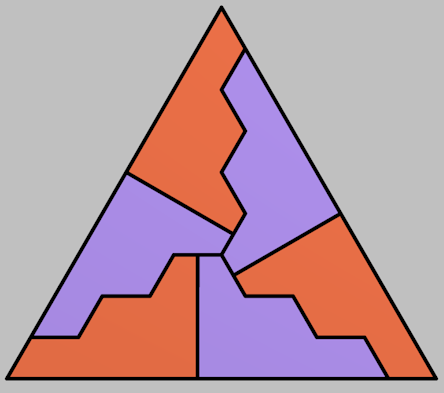
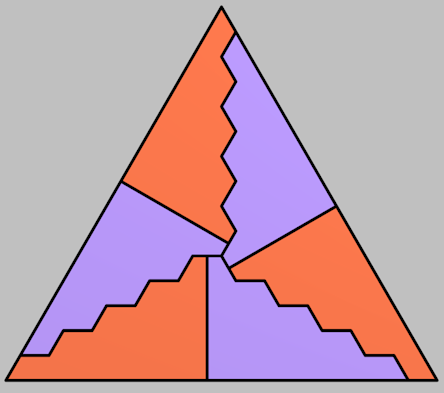
Here's the next one:

Click to reveal a tricker solution

The pattern is starting to form, but may not be obvious yet.

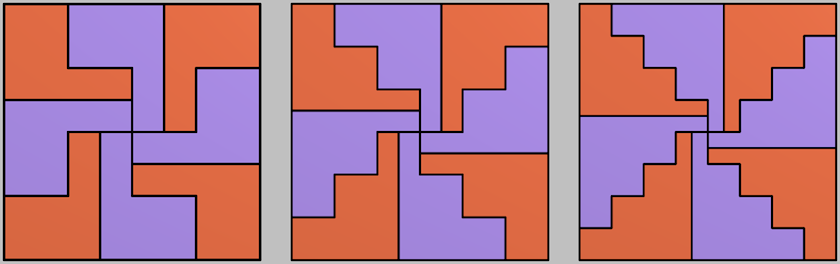
Here are the next three in the sequence, which should make it clear:

Click to reveal more solutions

Someone asked whether it extended to other regular polygons. The answer is yes, but only for squares and pentagons. For hexagons and beyond the zigzags hit each other, and the zigzags must follow certain angles for this to work.

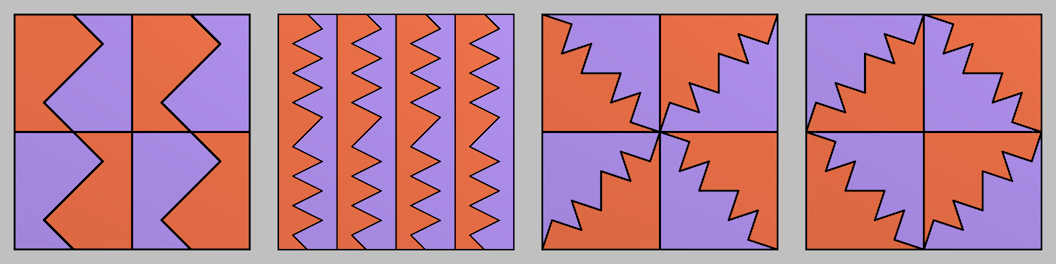
Here's what it looks like for squares.

Click to reveal subdivided squares

Note: there are other trivial ways to cut a square into 8 congruent pieces, and even other infinite series of ways. Here are some examples, each representing one of an infinite series.

Click to reveal more subdivided squares

And here's the solution for pentagons, each cut into 10 congruent parts.

Click to reveal subdivided pentagons

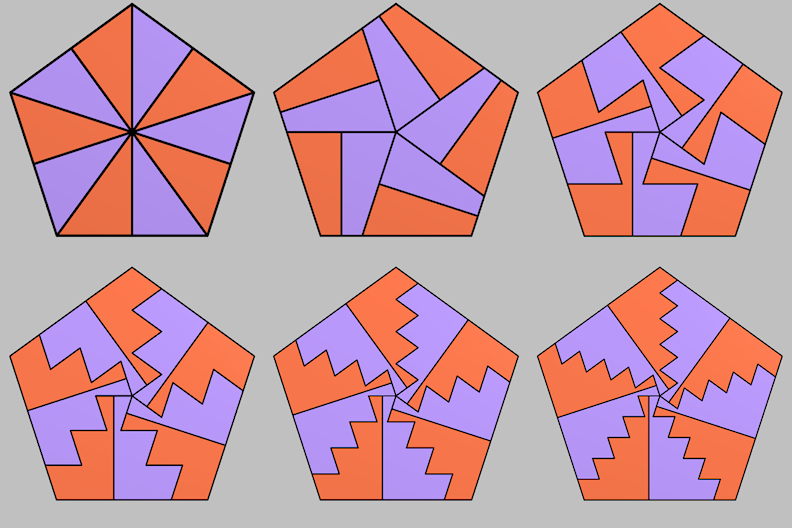
I am not sure if this is a new discovery (posted on 29 June 2025). It's hard to search for this sort of thing without just finding endless references to the simplest way. If anyone has seen this before, let me know.

Home > Research > Consistent Vertex Descriptions
Prev (Augmented Uniform Polyhedra)	Next (Vertex Descriptions)