Home > Gallery > My Models > Cupolae > Crossed Square Cupola
Prev (Augmented Great Cubicuboctahedron)	Next (Crossed Pentagrammic Cupola)

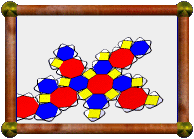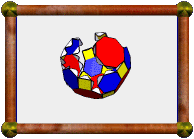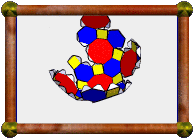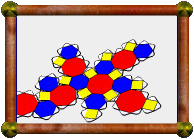
Crossed Square Cupola

An n/d cupola has a top which is an n/d-gon with squares attached to each side. The squares connect to every second edge of the base, which is a 2n/d-gon. The other edges attach to triangles which fill in the gaps and complete the model.

For example, the square cupola is a Johnson solid (J4). A square is a 4/1-gon, so the cupola's base is an 8/1-gon, ie an octagon.

The model presented here is a 4/3 cupola. A 4/3-gon is a retrograde square, ie a normal square, but we visit the four vertices in the opposite order. So the base is an 8/3-gon, which is an octagram, as you can see in the picture.

Home > Gallery > My Models > Cupolae > Crossed Square Cupola
Prev (Augmented Great Cubicuboctahedron)	Next (Crossed Pentagrammic Cupola)