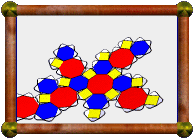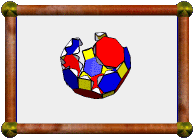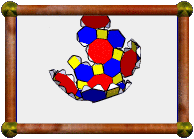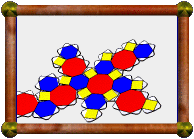
Compound of 5 Dodecahedra

Like or comment on facebook

	Here we see how a cube may fit inside a dodecahedron. There are five ways to fit the cube in, which gives us the familiar compound of 5 cubes. On the other hand, there are two ways to fit a dodecahedron around a given cube. Consider fitting these dodecahedra around each cube in the 5-cube compound. One of the two orientations is just the original dodecahedron in which we fitted the 5 cubes, but if we use the other orientation instead, we get the compound of 5 dodecahedra.
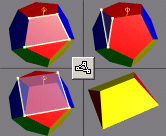
	Note above that the dodecahedron can be created by augmenting each face of a cube with a roof-shaped cap. So one way to create the 5-dodecahedron compound in Great Stella is to start with the 5-cube compound and augment each side with such a cap. To make the cap, start with the dodecahedron, drop to the "2-fold pyramidal" symmetry group, and create the three facets shown (using Create Facets Mode). Then use "Poly>Create Faceted Model" to create the cap. Use "Edit>Put Model in Memory>Memory 1" to put the model in memory. Then load the 5-cube compound and use "Poly>Augment Polyhedron" (or just hit "a"), choosing memory slot 1 as the source, to augment the model's faces with the cap.
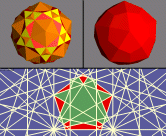
	Another way to make this model is to start with the icosidodecahedron and use "Poly>Add Base Model and Dual" (shown top left). Then create the convex hull of this model using "Poly>Create Convex Hull" (top right). This may look like the strombic hexecontahedron, but is really a slightly distorted version. It turns out that the 5-dodecahedron compound is a stellation of this model, so just find the appropriate 2D regions in the stellation diagram.
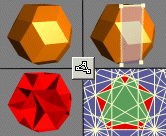
	Yet another way this model could be made is to start with the rhombic triacontahedron and use Create Facets Mode to create the facet shown (top right). Then use "Poly>Create Faceted Model" to create the model shown bottom left. It is one of only four isohedra with rectangular faces. Again, the 5-dodecahedron compound lies in the stellation pattern of this model.
	With any of the above methods, there's a couple of things you want to do at the end to finish it off. Firstly, it would be nice to see the dual compound of 5 icosahedra (shown top left). You can't do this yet because, although the model may look right, its faces are not truly pentagons yet. Use Create Facets Mode again to create the facet shown (top right, a single pentagon). Then use "Poly>Create Faceted Model" to create the true model, consisting of intersecting pentagons. Finally, the model will currently be displayed in only a single color (bottom left), because all faces are of the same type. Use "Color>Color as a Compound" to automatically color each of the five components differently (bottom right).
	At the time I found that the model doesn't really need any additional internal support to keep it solid, but in hindsight I wish I'd strengthened it a bit. Tends to dent if not careful. To finish the model, leave a hole like this.
	This cap can then be made and glued over the hole.

Home > Gallery > My Models > Symmetric Compounds > Compound of 5 Dodecahedra
Prev (Compound of 5 Cubes)	Next (Compound of 2 Small Stellated Dodecahedra)