Dodecahedron

• Vertex description: 5.5.5
• Faces: 12
• Edges: 30
• Vertices: 20
• Dual: Icosahedron
• Stellations:
  • Fully supported: 4 (4 reflexible, 0 chiral)
  • Miller's rules: 4 (4 reflexible, 0 chiral)

One of the five regular convex polyhedra known as the Platonic solids. This model was made from a single connected net, printed on one sheet of A4 paper. Nets can be generated and printed at any size using any of Small Stella, Great Stella, or Stella4D, even in the free demo versions.

Above is a dodecahedron with photos of a cat on each face (seen from above, below, and in original net form). Stella allows you to map photos onto faces in 3D. The images then appear on nets when you print them out, ready to be cut out, folded up, and glued together as seen here.

Here's another model. This time the photos were fitted inside each face, rather than around each face, so a border is visible.

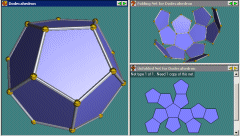
Here's a dodecahedron in Stella, using a 3-view layout featuring the dodecahedron itself, the unfolded net, and a partially folded net. See more screenshots here.

	Here is a compound of the dodecahedron with its dual. Notice how the dodecahedron's vertices sit above the icosahedron's faces, and vice versa? Also the edges of the two polyhedra bisect each other at right-angles.
	Multiple dodecahedra can be arranged in an intersecting manner to form various compounds. Here is one consisting of 5 intersecting dodecahedra.
	The dodecahedron has three stellations. Here is the first, the small stellated dodecahedron. It's also a faceting of the icosahedron.
	Second stellation, the great dodecahedron. This one is also a faceting of the icosahedron.
	Third and final stellation, the great stellated dodecahedron. This is also an example of a faceting of the dodecahedron. The dodecahedron has quite a few facetings. You should be able to see that this polyhedron's vertices are the same as that of a dodecahedron (this is all faceting means).
	Some of its facetings are compounds of other Platonic solids, such as this compound of 5 cubes.
	The compound of 5 tetrahedra is another well-known faceting.
	The compound of 10 tetrahedra is yet another well-known faceting.
	Subsymmetric stellations are also possible. These are stellations that have less symmetry than the dodecahedron itself. The polyhedron shown here is an example. It's hard to tell looking at it, but this polyhedron's faces lie in the same planes as the faces of a regular dodecahedron (this is what makes it a stellation).
	Another subsymmetric stellations of the dodecahedron. This one highlights the relationship between the three fully symmetric stellations, with the spikes of the final stellation (great stellated dodecahedron) visible outermost, but with some missing to reveal the inner stellation layers, and the small stellated dodecahedron showing inside.

Home > Gallery > My Models > Platonic Solids > Dodecahedron
Prev (Octahedron)	Next (Icosahedron)