Cubohemioctahedron

Like or comment on facebook

• Vertex description: 4.6.4/3.6
• Faces: 10
• Edges: 24
• Vertices: 12
• External facelets: 30
• Dual: Hexahemioctacron (infinite)
• Name breakdown:
  • Cubo-: 6 faces (squares) lie parallel to those of a cube
  • -hemi-octa-: Hemi = through the centre of model. Octa = faces (hexagons) parallel to an octahedron, but only half as many (4) because they're hemi

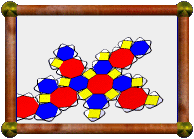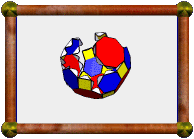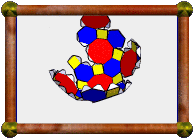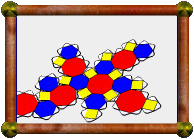
A uniform polyhedron whose faces consist of 6 squares (orange) and 4 hexagons (each a different colour). It is a faceting of the cuboctahedron, that is, it shares the same vertices. It also shares the same vertices with the Octahemioctahedron. In fact these all share the same edges too.

Nets for this model were printed from Great Stella using a colour inkjet printer onto white paper. I think the result looks better than those printed with a colour laser printer. The colour doesn't crack at the edges so much.

	One of the nets from Great Stella. I used the "Edge connection IDs" option from the print-preview dialog box, which numbers all the tabs in matching pairs. This is useful to make sure you arrange the colours correctly.
	Start by gluing one of the six pyramids together with the tabs out. Then find another one with a matching tab number, such as 22 seen here.
	The tabs should be folded in and glued around the matching pair of tabs that were already glued facing out. Tabs without a match yet should be folded and glued out.
	Proceed with the remaining pyramids, folding any tab-pair in if they have a match already and gluing around that matching tab-pair, or folding and gluing out if not matched yet.
	Last part. You'll need to apply glue carefully to all remaining tabs and put this part in place all at once.
	Another view of the finished model.

Home > Gallery > My Models > Uniform Polyhedra > Cubohemioctahedron
Prev (Octahemioctahedron)	Next (Small Cubicuboctahedron)