Cube

One of the five platonic solids, and dual of the octahedron. The one polyhedron everyone is familiar with! This model was made from a single connected net, printed on one sheet of A4 paper. Nets can be generated and printed using any of Small Stella, Great Stella, or Stella4D, and is even available in their free demo versions.

Here's how an cube might look in Stella. You can see more screenshots here.

	Here is a compound of the cube with its dual.
	Multiple cubes can be arranged in an intersecting manner to form various compounds. Here is one consisting of 3 intersecting cubes.
	Here is another compound consisting of 4 intersecting cubes.
	Here's the best-known cube compound, consisting of 5 intersecting cubes.
	The cube has no stellations but it does have one fully symmetric faceting, shown here. You can see that it has the same vertices as a cube. This faceting is also a compound of two tetrahedra and a stellation of the octahedron.
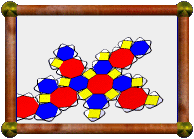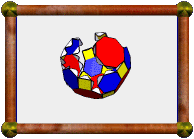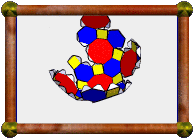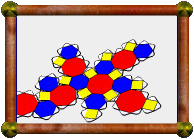
	The cube also has subsymmetric facetings, meaning they have less symmetry than the cube itself. Here is an example. Again, you can see that it has the same vertices as a cube.

Home > Gallery > My Models > Platonic Solids > Cube.
Prev (Tetrahedron)	Next (Octahedron)