| Small Hexacronic Icositetrahedron / Small Rhombihexacron |

This model represents the duals of two different uniform polyhedra.
The small hexacronic icositetrahedron is dual of the
small cubicuboctahedron,
while the small rhombihexacron is dual of the
small rhombihexahedron.
The two duals have the same external appearance, but edges are traversed
differently around their faces. The first has arrow-head-shaped faces, while
the second has butterfly-shaped faces. The differences being hidden from view
by other faces.
The kaleidoscopic effect is made up from photographs of one of my
cats, repeated symmetrically. When a photo is applied to several faces,
Great Stella
uses mirror images on mirrored faces, to help produce results like this.
|
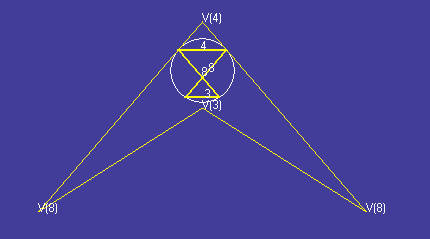
Vertex figure of the
small cubicuboctahedron (thicker
yellow lines in the centre) with
Dorman Luke construction of the
dual's face (thinner yellow lines around the outside). As seen in
Stella's vertex figure view.
|
|
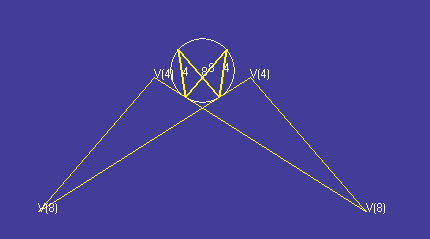
Vertex figure of the
small rhombihexahedron (thicker yellow lines in
the centre) with
Dorman Luke construction of the
dual's face (thinner yellow lines around the outside).
See how the duals' faces have the same long arms pointing down. The
differences between the faces are hidden inside the solid model.
The shared vertices at the end of those long arms correspond to the
shared octagonal faces of the two uniform polyhedra.
|

|
Here's what the nets look like printed out.
|

|
Score the edges, cut the nets out, fold the edges, and see what your
cat thinks.
|

|
Each part folds into a peak, and these peaks are then glued together.
To keep the model solid, I added these green triangles inside. You can
make these easily using Stella's Faceting mode.
|

|
One peak left to go.
|

|
Add the green internal supports around the hole, and around the final
peak. Then glue can be applied and the final peak pushed into place.
|

|
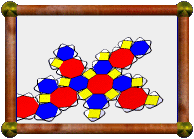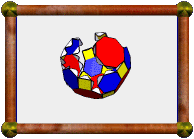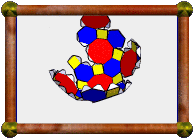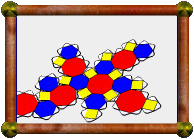
Here's a topological version of the small hexacronic
icositetrahedron. In this version parts of each
face have been cut away so that only faces that truly share an edge are
still connected. Where two faces would normally intersect to cause a
false edge, now they weave through each other without collision.
It's not a model of the small rhombihexacron, because now we can
see inside to the otherwise hidden parts of the faces.
|