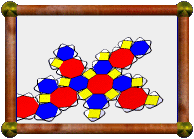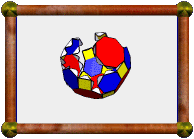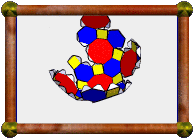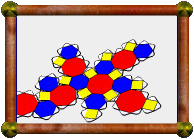
Pseudo Great Rhombicuboctahedron

Like or comment on facebook

• Vertex description: 4.3/2.4.4 (but non-uniform overall)
• Faces: 26
• Edges: 48
• Vertices: 24
• External facelets: 424
• Dual: Pseudo great strombic icositetrahedron
• Name breakdown:
  • Pseudo: A non-uniform variation, only possible with two uniform polyhedra.
  • Great Rhombicuboctahedron: The uniform polyhedron being varied. See great rhombicuboctahedron.

This is the pseudo version of the great rhombicuboctahedron. See the pseudo rhombicuboctahedron for a simpler example of a pseudo-uniform polyhedron (they are actually topologically identical to these more complex models!). Here again, the pseudo model may be thought of as having one section twisted with respect to the true uniform model, but it is much harder to visualise, and the vertices are still all surrounded by faces in the same way (three squares and one retrograde triangle). The symmetry group of the pseudo model is 4-fold dihedral, same as that of the square antiprism.

This model is the dual of the pseudo great strombic icositetrahedron.

To get this model in Great Stella, start by selecting the "Great Rhombicuboctahedron" from the list, then select the "Poly>Create Pseudo Version" menu item.

	Here you see one of each different type of net required to build the model. There are a lot!
	And here are all the nets. A box with compartments helps a lot to keep the pieces organised. As you can see, there aren't enough compartments for all the different kinds of pieces, but I group pieces together that will be directly connected. The great rhombicuboctahedron may have slightly more external facelets (488 versus 424), but this model is a bit trickier to construct. The smallest pieces are smaller, and there's certainly more variety along the way.
	As with the non-pseudo version, we start by building one of these octagram parts. Note the different colour arrangement however, and you only need two of these parts, rather than six.
	Next put together four of this part.
	You'll also need four of these parts (shown here in stages of completion).
	The above eight parts can then be glued around one of the octagram parts, as shown. The model so far has a big green square as its base.
	Here is the same thing upside-down. The big green square stands out. The next set of parts will be glued around each edge of this green square.
	The two nets shown here fold up to create pieces that are mirror images of each other, but note that the cut required to flatten the net is along a different edge. By default, Great Stella creates both nets like the one on the right, but cutting the shorter edge like the one on the left leads to nets that pack better onto the page when printing, and the edges requiring gluing are shorter. So I used "Selection>Mouse Selection Mode>Cut/Uncut Edges" mode, and then Shift+Left-Click on the shorter edge of one of these pieces, to cut that edge instead of the longer one. Only do this to one of the two nets though, since the longer tabs from the other net will be useful for gluing behind other faces later.
	Put together these pieces as shown.
	And these in turn go together to make this part. You will see now how that long tab is used to glue the deep sections together behind the big yellow face. You need to make four of these.
	Glue those four parts to the four edges of the big green square from earlier. I have also glued an extra piece of paper along each edge for added strength.
	These four parts then fold up and glue in place using more of those long tabs.
	Now fill in the gaps around this level, leaving a big square around the opening.
	Then add everything except for the second octagram part and its four surrounding yellow triangle pairs, to get what's shown here. Most of this can be constructed separately, and then glued on in just a few parts. Finally, glue the octagram part in place, same as the last octagram part of the great rhombicuboctahedron was, and add the final four yellow triangle pairs to complete the model.
	The view down a 4-fold rotational symmetry axes.
	The view down a 2-fold rotational symmetry axes.

Home > Gallery > My Models > Uniform Polyhedra > Pseudo Great Rhombicuboctahedron
Prev (Great Rhombicuboctahedron)	Next (Cubitruncated Cuboctahedron)