One of the four Kepler-Poinsot solids. It consists of twelve
intersecting pentagrams. As the name suggests, it is a stellation of the
dodecahedron. It is also a faceting of the
icosahedron.
|
First, a tip about folding. After scoring all the edges and cutting
out the net, I suggest folding the long edge shown before cutting the
wedge out at its centre. It may not fold as evenly towards the tapered
ends when that wedge is gone.
|
|
I use a pentagon at the base of each spike to add rigidity.
|
|
Finally, assemble the parts as you would a dodecahedron.
|
|
A stack of these models can be made, each scaled by the
golden ratio with respect to the
next one in the stack. The models fit together perfectly, and various
points, lines, and planes align with each other as if by magic.
|
|
Here is the same stack viewed from above. Even the shadow is
interesting!
|
|
Here's a topological version. In this version parts of each
face have been cut away so that only faces that truly share an edge are
still connected. Where two faces would normally intersect to cause a
false edge, now they weave through each other without collision.
|
|
Here is a compound of two small stellated dodecahedra, having overall
octahedral symmetry.
|
|
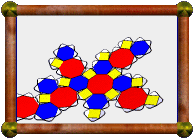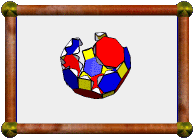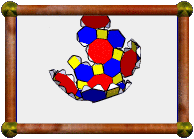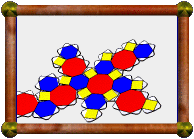
And a compound of five small stellated dodecahedra, having full
icosahedral symmetry overall.
|
