Compound of 10 Tetrahedra

Home > Gallery > My Models > Symmetric Compounds > Compound of 10 Tetrahedra
Prev (Compound of 5 Tetrahedra)	Next (Compound of 5 Octahedra)

Compound of 10 Tetrahedra

Like or comment on facebook

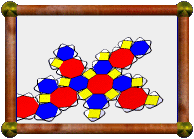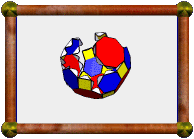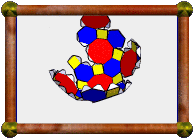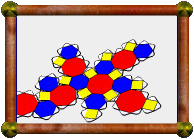
Another classic compound is the compound of 10 tetrahedra. The compound of 5 tetrahedra is chiral, i.e. it doesn't have any mirror symmetry and comes in left- and right-handed versions. If you combine these together you get this compound of 10 tetrahedra. You may also think of this as a compound of 5 stella octangula (5 compounds of 2 tetrahedra).

Can you spot a tetrahedron in each color? This model is made in 10 colors, one for each tetrahedron. But I also grouped the colors roughly into two sets of 5, one lighter and one darker, each representing one compound of 5 tetrahedra. Doing this means that dark only touches light and vice versa. I also went for matching pairs between the sets:

Light blue and dark blue
Light green and dark green
Light pink and dark red
Light silver and dark grey
Light yellow and dark purple (ran out of matching paper colors here!)

Each pair represents a stella octangular. This also guarantees that the light and dark versions of colors never touch each other.

You could also make interesting models with either 5 colors or just 2 colors. 5 colors would highlight each stella octangula, or 2 colors would highlight the two mirror image compounds of 5 tetrahedra.

The compound is also a stellation of the icosahedron (the facial planes carve out an icosahedron at the centre), and a faceting of the dodecahedron (they share the same vertex positions).

The model and the nets required to build it are available in Small Stella, Great Stella and Stella4D's Polyhedron Libraries. This paper model is 14cm in diameter.

Start gluing the parts together, but be very careful to get the color arrangement right!

I used Stella's Faceting mode to create some extra pieces to fit inside and add strength, seen here in white.

About half-way. Keep adding the internal parts as long as you can still reach inside. Make sure you have some angled needle-nose tweezers!

When arriving at the last 5 peaks, you'll need to proceed a little differently. From this point, I made the 5 peaks individually, along with those internal pieces to hold their shape on each side. You can then glue these in one by one.

Here's a close-up of those final pieces.

Home > Gallery > My Models > Symmetric Compounds > Compound of 10 Tetrahedra

Prev (Compound of 5 Tetrahedra) Next (Compound of 5 Octahedra)

	Start gluing the parts together, but be very careful to get the color arrangement right!
	I used Stella's Faceting mode to create some extra pieces to fit inside and add strength, seen here in white.
	About half-way. Keep adding the internal parts as long as you can still reach inside. Make sure you have some angled needle-nose tweezers!
	When arriving at the last 5 peaks, you'll need to proceed a little differently. From this point, I made the 5 peaks individually, along with those internal pieces to hold their shape on each side. You can then glue these in one by one.
	Here's a close-up of those final pieces.